反函数的定义,反函数概念解析与应用探讨

反函数是一个数学概念，它描述了函数的逆操作。对于一个函数 f，如果存在另一个函数 g，使得对于 f 的定义域中的每一个元素 x，都有 gqwe2 = x 和 fqwe2 = x，那么函数 g 就被称为函数 f 的反函数。

反函数的存在需要满足一定的条件。首先，函数 f 必须是一对一的，即对于定义域中的任意两个不同的元素 x1 和 x2，都有 f ≠ f。其次，函数 f 的值域必须是实数集或者实数集的一个子集。

反函数的定义可以简单理解为：如果函数 f 将元素 x 映射到元素 y，那么反函数 g 将元素 y 映射回元素 x。反函数的存在和定义使得函数具有可逆性，即可以撤销函数的映射操作。

需要注意的是，并不是所有的函数都存在反函数。只有满足一对一条件的函数才有可能存在反函数。此外，反函数的存在还与函数的定义域和值域有关。亲爱的数学迷们，今天我们要来聊聊一个听起来有点神秘，但实际上非常有趣的数学概念——反函数。想象你有一个神奇的镜子，可以把你手中的苹果变成苹果汁，再把你手中的苹果汁变回苹果。这个镜子在数学里就相当于反函数，它能让你的数学世界变得更加丰富多彩。那么，什么是反函数呢？让我们一起揭开它的神秘面纱吧！

什么是反函数？

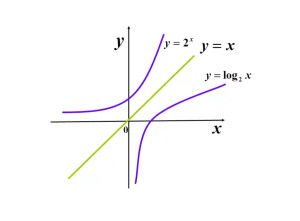
简单来说，反函数就是原函数的“镜像”。如果你有一个函数f(x)，那么它的反函数g(y)就是这样一个函数，它能够把f(x)的输出值y变回输入值x。换句话说，如果你用f(x)把x变成了y，那么用g(y)就能把y变回x。

举个例子，假设你有一个函数f(x) = 2x 3，这个函数的意思是，如果你把x代入，就能得到一个y值。比如，当x=2时，y=7。现在，我们要找到这个函数的反函数。首先，我们把y和x的位置交换，得到x = 2y 3。我们解这个方程，得到y = (x - 3) / 2。所以，这个函数的反函数就是g(y) = (y - 3) / 2。

反函数的来源

反函数的概念源于对函数的单射性和满射性的研究。一个函数如果在其定义域内是严格单调的，并且是单射（每个y值对应唯一的x值）和满射（覆盖了整个值域），那么它的反函数就存在。

想象如果你有一个函数，它的图像是一条直线，而且这条直线不会在任何一个点与x轴或y轴相交两次，那么这个函数就满足单射和满射的条件。这样的函数就可以找到一个反函数。

如何求反函数？

求一个函数的反函数通常遵循以下步骤：

1. 交换x和y：将原函数的方程中的x和y交换位置。

2. 解出y：解出y关于x的表达式。

3. 确定反函数的定义域和值域：反函数的定义域是原函数的值域，反函数的值域是原函数的定义域。

举个例子，假设我们要找到函数f(x) = x^2的反函数。首先，我们交换x和y，得到x = y^2。我们解出y，得到y = √x。但是，我们还需要确定反函数的定义域和值域。由于原函数f(x) = x^2的定义域是所有实数，值域是非负实数，所以反函数的定义域是非负实数，值域是所有实数。

反函数的应用

反函数在数学和现实世界中有着广泛的应用。在数学领域，反函数用于解决方程和不等式，是微积分中重要的工具。在现实世界中，反函数可以应用于各种场景，比如解码加密信息，计算物理现象的反向过程，以及工程和科学问题中的逆向运算。

举个例子，如果你知道了一个物体的速度v和时间t的关系，即v = f(t)，那么你可以使用反函数来找到物体在某个特定时间t的位置。这就像是用那个神奇的镜子，把速度变回时间，再变回位置。

反函数是数学中一个深刻且实用的概念，它不仅丰富了函数理论，也为实际问题提供了解决方案。通过学习反函数，我们可以更好地理解函数的本质，以及它们在现实世界中的应用。所以，下次当你看到那个神奇的镜子时，不妨想想它背后的数学原理，也许你会对反函数有更深的认识。